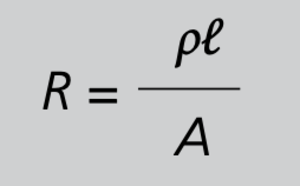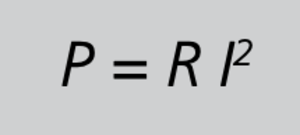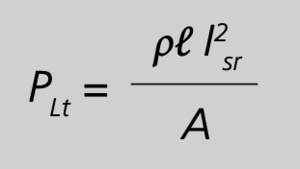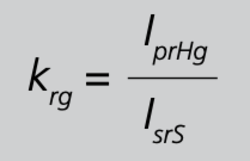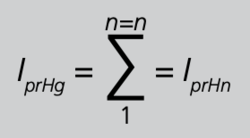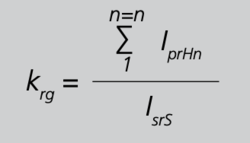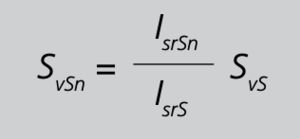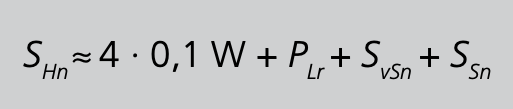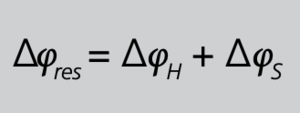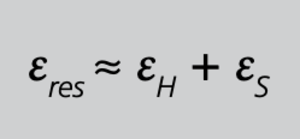7. PRAKTISCHE ANWENDUNG VON STROMWANDLERN
7.1 BEISPIEL ZUR BESTELLUNG EINES STROMWANDLERS
An einem konkreten Beispiel, bei dem der Anwender die Ströme in den drei Strängen des Drehstromsystems 230/400 V, 50 Hz eines 80 kW- Generators messen muss, sollen die Bestellparameter gezeigt werden. Die Berechnung liefert einen Strom nach Gleichung 20/S.83
Gleichung 20

von 115,94 A, der indirekt mittels Stromwandler gemessen werden soll. Wenn ein Stromwandler mit der Bemessungsübersetzung 115,94/5 A auch technisch möglich ist, so würde es bestimmt schwierig sein, ein Messgerät derart zu skalieren, dass es bei einem Strom von 5 A den Primärstrom 115,94 A anzeigt. Bei Analoginstrumenten halten die Lieferanten Wechselskalen vor, die den genormten Bemessungsübersetzungen von Stromwandlern entsprechen. Digitalinstrumente sind da zwar etwas flexibler, da bei skalierbaren Instrumenten beliebige Wandlerfaktoren einprogrammieren werden können. Man würde sich aber hier für Stromwandler mit der Übersetzung 125/5 A , entscheiden, wobei es sich dabei um den nächstgrößten genormten Wert nach 115,94/5 A handelt. Der nächste Schritt besteht darin, die geometrisch passenden Stromwandler nach dem Querschnitt des Primärleiters festzulegen. Hat man es mit einem starren Schienensystem zu tun, so ist auch noch die Wandlerbreite anhand des Schienenabstands zu beachten. In diesem Beispiel ist ein Kabel mit 95 mm2 Kupferquerschnitt eingesetzt. Man soll einem Lieferanten für Stromwandler aber nicht den Kupferquerschnitt vorgeben, da er nicht wissen kann, wie stark im vorliegenden Fall die Isolation ist. Da sich in diesem Beispiel für den Kabeltyp H07RN-F entschieden wurde, beträgt der Durchmesser 23,3 mm. Um nun den Stromwandler leicht und reibungsfrei über das Kabel schieben zu können, sollte dieser eine Primärleiteröffnung von mindestens 26 mm haben. Nun kann man sich Gedanken machen über die angeschlossene Bürde, einschließlich der Zuleitungen zum Messgerät. Es wurde ein Abstand zum Messgerät von 5 m ermittelt, also mit Hin- und Rückleiter l =10 m. Das Messgerät selbst soll eine Bürde von 1,5 VA haben. Mit dem vorgegebenen Drahtquerschnitt (hier von 2,5 mm2) bestimmt man nach
ρ = spezifischer Widerstand bei 20 °C
Cu:= 0,0171 Ωmm2 ⁄ m [1]
Al: = 0,0279 Ωmm2 ⁄ m [1]
PLr= Leistungsbedarf der Messleitung bei sekundärem Bemessungsstrom
l = Leitungslänge (Hin- und Rückleiter)
I2sr = sekundärer Bemessungsstrom sr
A= Leiterquerschnitt
[1] Datenblatt Elektrisola (http://www.elektrisola.com/de/leitermaterial/kupfer.html)
die Leistung, die die Sekundärleitung „verbraucht“. Da diese Leistung zur Berechnung der einzusetzenden Bemessungsleistung des Stromwandlers herangezogen wird, versteht es sich von selbst, dass der hier zur Anwendung kommende Strom der sekundäre Bemessungsstrom sein muss. Die so ermittelte Leistung beträgt PLr=1,78 W. Dazu muss die Leistungsaufnahme des Messgeräts von 1,5 VA plus einem Sicherheitszuschlag von viermal 0,1 W für eventuelle Übergangswiderstände an den vier Anschlussklemmen (zwei Klemmen am Wandler, zwei Klemmen am Messgerät) addiert werden. So folgt die vom Wandler zu fordernde Leistung Sb = 3,68 VA . Man wählt die nächste genormte Bemessungsleistung von Sr= 5 VA . Da aber ohnehin die errechnete Leistung auf die nächstgelegene genormte Bemessungsleistung aufgerundet wird, ist übertriebene Genauigkeit hier fehl am Platze. Als Genauigkeitsklasse reicht in diesem Beispiel für eine normale Betriebsmessung die Klasse 1. Mit Rücksicht auf die Belastung des Messkreises im Fehlerfall wird der Überstrom-Begrenzungsfaktor FS 5 gewählt. Da man auch nicht über den gewählten Bemessungsstrom von 125 A hinaus messen will, fällt die Entscheidung für den üblichen Bemessungs-Dauergrenzstrom von 120%.
Nun liegen die Bestelldaten für drei Stromwandler wie folgt fest:
a) Art des Wandlers: Aufsteck-Stromwandler
b) Wandlertyp: Bezeichnung herstellerabhängig anhand der Geometrie und der Primärschienenöffnung von ≥ 26 mm Ø
c) Bemessungsübersetzung: 125/5 A
d) Bemessungsleistung: 5 VA
e) Genauigkeitsklasse: Kl.1 FS 5 ext.120 %
Damit sind nun alle relevanten Daten für den Wandlerlieferanten bestimmt.
7.1.1 WIDERSTÄNDE VON SCHALTDRÄHTEN, LEISTUNGSAUFNAHME VON MESSGERÄTEN UND RELAIS
Für eine schnellere Handhabung in der Praxis sind in Tabelle 4/S.87 die Widerstände der im Schaltanlagen- und Verteilerbau eingesetzten Drähte angegeben, entsprechend der DIN VDE 0295. Da die Nennquerschnitte Schwankungen unterworfen sind, handelt es sich hier jeweils um die höchstmöglichen Widerstandswerte. Diese weichen daher gering von den berechneten Werten nach Gleichung 21/S. 84 ab. Tatsächlich sind diese Differenzen bei den hierbei geforderten Genauigkeiten aber unbedeutend.
| Nennquerschnitt in mm² | Widerstände bei 20 °C in Ω/m | Leistungsverluste bei 5A in W/m | Leistungsverluste bei 1 A in W/m | |||
|---|---|---|---|---|---|---|
| Klasse 1+2 | Klasse 5 | Klasse 1+2 | Klasse 5 | Klasse 1+2 | Klasse 5 | |
| 1 | 0,0181 | 0,0195 | 0,4525 | 0,4875 | 0,0181 | 0,0195 |
| 1,5 | 0,121 | 0,0133 | 0,3025 | 0,3325 | 0,0121 | 0,0133 |
| 2,5 | 0,0074 | 0,00798 | 0,185 | 0,1995 | 0,0074 | 0,00798 |
| 4 | 0,00461 | 0,00495 | 0,11525 | 0,12375 | 0,00461 | 0,00495 |
| 6 | 0,00308 | 0,0033 | 0,077 | 0,0825 | 0,00308 | 0,0033 |
Was die Leistungsaufnahme von Messgeräten betrifft, so reicht es auch schon, diese abzuschätzen. Eine Unterstützung dabei liefert Tabelle 5/S.89.
| Messgeräte | S/VA |
|---|---|
| Dreheisen-Strommesser | 1 |
| Drehspul-Strommesser | 1 |
| Bimetall-Strommesser | 2 - 2,5 |
| kombinierter Bimetall-Strommesser (Dreheisen mit Bimetall) | 3 - 4 |
| schreibende Strommesser | 0,5 - 9 |
| Leistungsmesser (je Strompfad) | 0,5 - 3 |
| schreibende Leistungsmesser (je Strompfad) | 0,5 - 5 |
| Leistungsfaktormesser (je Strompfad) | 2 - 5 |
| Stromzähler (je Strompfad) Wirk-, Blind- oder Scheinleistung | 0,5 - 4 |
In die Klasse 1 fallen eindrähtige, also massive Leitungen. Die Klasse 2 enthält sogenannte mehrdrähtige Litzen. So hat z. B. eine Leitung mit dem Nennquerschnitt von 2,5 mm2 7 Einzeldrähte mit je 0,52 mm Durchmesser. Zur Klasse 5 gehören feindrähtige Litzen. Hier findet man z.B. bei dem Nennquerschnitt von 2,5 mm2 30 Einzeldrähte mit je 0,25 mm Durchmesser.
7.2 DURCHSCHLEIFEN MEHRERER MESSGERÄTE IM SEKUNDÄRKREIS
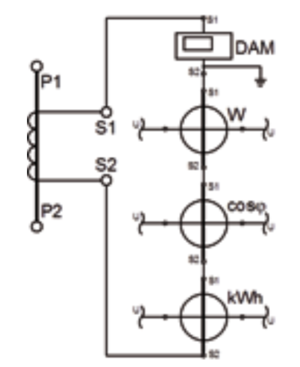
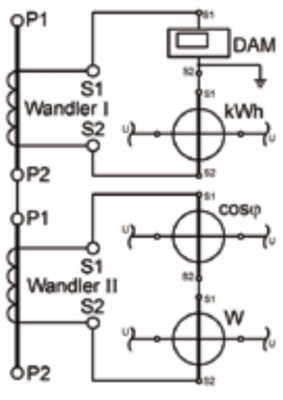
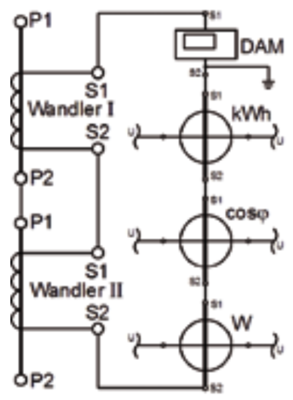
Seine Funktion als Konstantstromquelle erlaubt es, mehrere Messgeräte im Sekundärkreis eines Stromwandlers bis zum Erreichen der Bemessungsleistung in Serie anzuschließen, wie Abb. 25/S. 90 zeigt. In diesem Beispiel gelangt der Sekundärstrom über ein digitales Amperemeter (DAM) zu einem Wattmeter (W), weiter zu einem Leistungsfaktormesser (cosφ) und schießlich über einen Stromzähler (kWh) zurück zum Wandler. Die erforderlichen Spannungsanschlüsse der letzten drei Messgeräte sind nur angedeutet. Hier soll davon ausgegangen werden, dass das digitale Amperemeter intern an der S2-Klemme geerdet ist. Unter der Voraussetzung, dass der Leitungsverlust derselbe ist wie beim vorherigen Beispiel (PLr=1,78 W), müssen noch die Bürden der Messgeräte beachtet werden, die z. B. den Datenblättern der Messgerätelieferanten entnommen werden können. Nachfolgender Leistungsbedarf wurde für die Strompfade ermittelt:
digitales
Amperemeter: 0,1 VA
Wattmeter: 3 VA
Leistungsfaktormesser: 3 VA
Stromzähler: 5 VA
Obwohl die Leitungslänge unverändert ist, sollten jetzt aber die Übergangswiderstände von 10 Anschlussklemmen mit je 0,1 W berücksichtigt werden. So ergibt sich für die gesamte erforderliche Leistung der Wert 13,88 VA , wobei man sich wieder für die nächsthöhere genormte Bemessungsleistung von 15 VA entscheidet. Wie Abb. 25 / S. 90 auch zeigt, würde bei sekundärseitiger Erdung des Wandlers an der S1-Klemme das digitale Amperemeter über die Erdverbindung kurzgeschlossen. An einen Stromwandler können also mehrere Messgeräte in Serie angeschlossen werden, solange die Bemessungsleistung des Wandlers nicht überschritten wird. Es ist zu beachten, dass Mehrfacherdung vermieden werden muss.
7.3 LASTAUFTEILUNG AUF MEHRERE WANDLER
Gehen wir in einem weiteren Beispiel davon aus, dass der aus dem vorherigen Abschnitt geforderte Wandler mit 15 VA aus geometrischen oder physikalischen Gründen nicht herstellbar bzw. lieferbar ist, so bieten sich drei Möglichkeiten an, die Last auf zwei Wandler zu verteilen, um die Leistung zu erhöhen.
A) Messgeräte auf zwei Wandler verteilen
B) sekundäre Serienschaltung zweier Wandler
C) sekundäre Parallelschaltung zweier Wandler
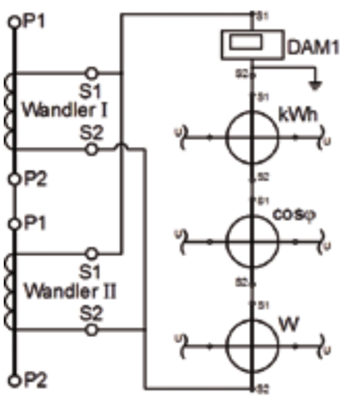
zu A) Man kann die Messgeräte sinnvoll bezüglich guter Leistungsaufteilung auf zwei gleiche, jedoch voneinander unabhängige Wandler verteilen, z. B. Wattmeter (W) und Leistungsfaktormesser (cosφ) auf Wandler I, digitales Amperemeter (DAM) und Stromzähler (kWh) auf Wandler II. Nachteilig hierbei ist, dass die doppelte Anzahl Zuleitungen zu den Messgeräten benötigt wird (wie in Abb. 26/S. 92 zu sehen). Vorteilhaft ist, dass einige Messgeräte (hier Leistungsfaktormesser und Wattmeter) von der Zwangserdung des Digitalinstruments entkoppeln werden. So ist zumindest Wandler II sekundär wieder erdfrei. Diese Lösung ist vorzuziehen, wenn im Sekundärkreis zwei Messgeräte Verwendung finden, die bereits intern geerdet sind, um diese gegeneinander zu entkoppeln.
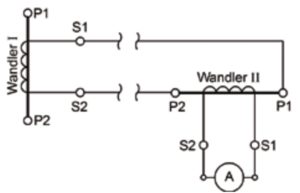
zu B) Eine Möglichkeit, die doppelten Zuleitungen zu vermeiden, ist die Serienschaltung der beiden Wandler (wie in Abb. 27/S.93). Dadurch addieren sich die Spannungen und auch folglich die Leistungen beider. Bei dieser Lösung ist zu beachten, dass sich zu der bereits vorhandenen Bebürdung eines Wandlers der Innenwiderstand des jeweils anderen Wandlers addiert. Diese Lösung sollte daher nur angewendet werden, wenn die Innenwiderstände beider Wandler hinreichend niedrig sind, also bei Aufsteckwandlern niedriger Übersetzung. Gegenüber der nächsten Lösung ist von Vorteil, dass keine Addition der Sekundärströme stattfindet, da Wandlerinstrumente nur für Ströme von 1 A oder 5 A erhältlich sind.
zu C) Letztlich besteht die Möglichkeit, beide Wandler sekundärseitig parallel zu schalten (Abb. 28/S34). Dadurch addieren sich allerdings die Ströme, sodass bei den 5 A-Ausgängen der Wandler letztlich in Summe 10 A fließen, was wiederum die Messgeräte überfordern würde. Um diese Problematik zu umgehen, kann man, statt der vorgesehenen Wandler mit der Übersetzung 125 / 5 A, Sonderwandler mit der Übersetzung 125 / 2,5 A einsetzen, auch wenn dieser Sekundärstrom nicht genormt ist. Diese Lösung ist trotz der möglichen Mehrkosten für Sonderwandler bei größeren Innenwiderständen der Wandler gegenüber Lösung B) vorzuziehen. Welcher dieser drei Lösungen letztlich der Vorrang zu geben ist, hängt also vom Einzelfall ab.
7.4 STROMWANDLER BEI GROSSEN SEKUNDÄRSEITIGEN LEITUNGSLÄNGEN
Es gibt Anwendungsfälle, bei denen die Entfernung zwischen Hauptwandler und Messgerät sehr groß ist. Dabei kann im ungünstigsten Fall der Widerstand der Messleitung (siehe auch Gleichung 21/S. 84) so hoch werden, dass die Bemessungsleistung des Stromwandlers überschritten wird. Vergrößern des Leitungsquerschnitts oder Verlegen mehrerer paralleler Leitungen zur Verringerung des Leitungswiderstands verbietet sich oft aus wirtschaftlichen oder geometrischen Gründen. Wie in Kapitel 3.10/S. 51 aber schon angedeutet, ist es bei größeren Leitungslängen im Messkreis vorteilhafter, Stromwandler mit einem sekundären Bemessungsstrom von 1 A einzusetzen. Gleichung 15/18 zeigt, dass die Leistung bei konstantem Widerstand quadratisch mit dem Strom zunimmt. Umgekehrt nimmt die Leistung natürlich quadratisch ab, wenn der Strom verringert wird. Hierzu soll wieder ein konkretes Beispiel betrachtet werden. Zwischen Wandler und Messgerät muss eine Leitung von 400 m (Hin- und Rückleiter) verlegt werden. Bei einem Querschnitt von 2,5 mm2 beträgt der Widerstand der Sekundärleitung 2,736 Ω. Der „Leistungsverbrauch“ auf dieser Leitung bei einem Sekundärstrom von 5 A beträgt dann nach Gleichung 15/18 immerhin 68,4 W. Einen Stromwandler mit einer Bemessungsleistung in dieser Größenordnung wird kaum zu finden sein. Wählt man nun hier einen Wandler mit dem sekundären Bemessungsstrom 1 A , so reduziert sich dieser „Leistungsverbrauch“ auf moderate 2,736 W . Ist der Leitungswiderstand größer, können selbstverständlich noch kleinere Sekundärströme gewählt werden, auch wenn es sich dabei dann nicht mehr um genormte Bemessungsströme handelt, so z.B. 0,5 A oder 0,1 A. Je nach Anzeige- oder Auswertegerät muss am Ende der Sekundärleitung der kleinere Strom mittels Zwischenwandler wieder auf eine genormte Bemessungsgröße transformieren werden, wie in Abb. 29/S.95 zu sehen. Die Verwendung von Strömen kleiner als 1 A hat zusätzlich den finanziellen Reiz, dass bei langen Leitungen deutlich dünnere Leitungsquerschnitte verwendet werden können.
7.5 SUMMEN-STROMWANDLER
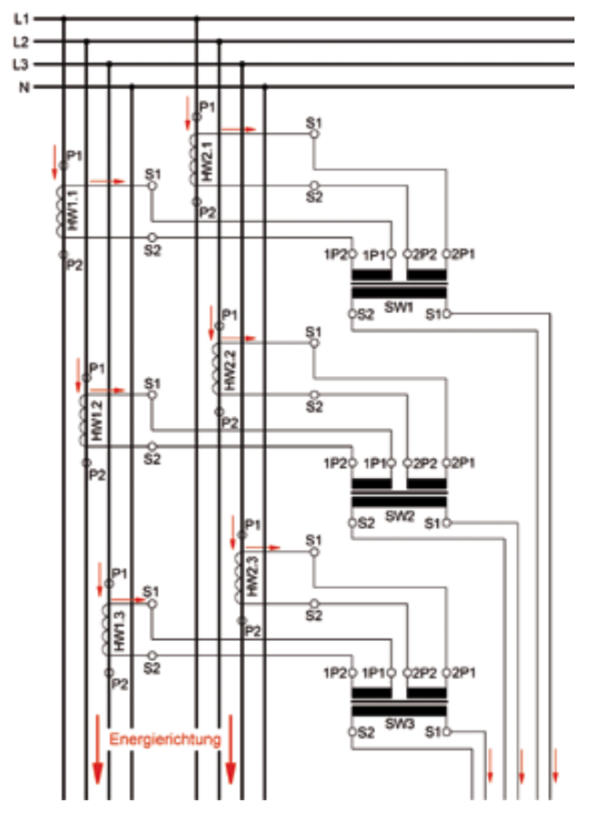
Die Problematik und die Besonderheiten beim Einsatz von Summen-Stromwandlern werden hier nur kurz behandelt. Das Buch „Strom-Messwandler, Informationen für Anwender“ widmet Summenwandlern ein ganzes Kapitel. Wie schon in Abschnitt 2.4/S. 24 erwähnt, sind sie Sonderformen von Wickelwandlern mit mehreren getrennten Primärwicklungen. Summen-Stromwandler werden i. Allg. nicht direkt an die Primärleiter angeschlossen. Ihr Betrieb erfolgt indirekt über Hauptwandler, die den zu messenden Strom in 1 A oder 5 A zur Speisung der Summenwandler umformen. Die genormten Bemessungsströme für die Ein- und Ausgänge von Summenwandlern sind 1 A und 5 A. Ein typisches Beispiel einer Beschaltung mit Summen-Stromwandlern zeigt Abb. 30/S.97. In diesem Beispiel werden die Ströme je Strang von zwei Abgängen der Sammelschiene addiert und der weiteren Messung zugeführt. Energie- und Stromrichtung sind durch rote Pfeile angezeigt. Ein Summenwandler addiert unter Berücksichtigung der Phasenlage die Primärströme von Verzweigungen desselben Strangs und ermöglicht dadurch die Messung der Summe der Ströme mit nur einem Instrument. Sekundärseitig wird durch die Konstruktion des Wandlers sichergestellt, dass die Ausgangsgröße i. d. R. wieder eine genormte Bemessungsgröße ist. Es lässt sich also von außen betrachtet sagen: Ein Summen- Stromwandler addiert die Eingangsströme und dividiert die Summe gleichzeitig durch die Anzahl der Eingänge.
Um seiner eigentlichen Aufgabe gerecht zu werden, ergibt es nur Sinn, Ströme in den Verzweigungen desselben Strangs zu addieren. Bei der Addition der drei Strangströme eines Dreiphasensystems würde die Summe der Ströme im fehlerfreien Betrieb null werden. In diesem Fall würde eine Fehlerstrommessung realisiert. Um diese Aufgabe zu erfüllen, gibt es jedoch besser geeignete Wandler (Abschnitt 2.4/S.24). Auch der Ausgang eines Summenwandlers muss immer kurzgeschlossen sein. Der Kurzschluss im bestimmungsgemäßen Betrieb erfolgt durch den niederohmigen Strompfad eines oder mehrerer Messgeräte. Gelegentlich kann es vorkommen, dass ein Eingang eines Summenwandlers nicht belegt ist. Unbenutzte Eingänge von Summen-Stromwandlern müssen dagegen immer offen bleiben. Ein kurzgeschlossener Eingang würde als zusätzliche Sekundärwicklung wirken mit der Folge, dass sich der Sekundärstrom auf beide Wicklungen aufteilt, was zu deutlichen Fehlmessungen führt. Hier ist besondere Achtsamkeit gefordert. Wird ein Eingang versehentlich kurzgeschlossen, kann das u. U. lange Zeit unbemerkt bleiben, da immer noch ein Sekundärstrom angezeigt wird.
7.5.1 KENNZEICHNUNG DER ANSCHLÜSSE UND TYPENSCHILD
Bei älteren Summenwandlern sind an den Sekundäranschlüssen noch die früheren Bezeichnungen k und l, manchmal schon in Kombination mit den Bezeichnungen S1 und S2 anzutreffen. Die Primäranschlüsse wurden mit Großbuchstaben in alphabetischer Reihenfolge benannt, in Verbindung mit K und L. So sieht man die Bezeichnungen AK und AL für den ersten Eingang eines Summenwandlers, BK und BL für den zweiten Eingang usw. Neuere Summen-Stromwandler haben sekundär nur noch die Bezeichnungen S1 und S2. Die Primärwicklungen werden dann mit 1P1 und 1P2 für den ersten Eingang, 2P1 und 2P2 für den zweiten Eingang usw. bezeichnet. Parallel dazu findet man primär auch die Benennung AP1 und AP2, BP1 und BP2 usw. Eine konkrete Vorschrift zur Klemmenbezeichnung von Summenwandlern ist zurzeit in keiner der Normen der Gruppe DIN EN 61869 zu finden. Das Typenschild eines Summen-Stromwandlers sieht grundsätzlich nicht anders aus als das eines üblichen Stromwandlers. Der einzige Unterschied liegt in der Benennung der Übersetzung. Diese wird auch hier wieder als ungekürzter Bruch genannt, wobei der Zähler die Eingangs-Bemessungsströme als Summanden enthält. Bei einem Stromwandler mit z.B. 3 Eingängen zu je 5 A und einem Ausgang von 5 A wird die Übersetzung also angegeben als 5+5+5/5 A. Aus Gründen der Übersicht wird manchmal bei einer größeren Anzahl von gleichen Eingängen statt der Summanden die Anzahl der Eingänge als Faktor angegeben, z. B. bei 9 Eingängen in der Form 9×5/5 A .
7.5.2 GESAMTÜBERSETZUNG krg , GESAMT-WANDLERFAKTOR cg
Um bei den nachfolgenden Betrachtungen Verwechslungen zwischen den Wandlern zu vermeiden, erhalten hier die Formelzeichen für Summenwandler den zusätzlichen Index S und die Formelzeichen für Hauptwandler den zusätzlichen Index H. Diese Indizierung ist nicht allgemein üblich und gilt nur für diese Abhandlung. Man unterscheidet Summenwandler hinsichtlich der Eingänge in Summen-Stromwandler für gleiche, sowie für ungleiche Hauptwandler. Haben alle Hauptwandler dieselbe Übersetzung, liegt der einfachste Anwendungsfall für Summenwandler vor. Um die Sekundärströme von Hauptwandlern mit unterschiedlichen Übersetzungen korrekt addieren zu können, müssen die Eingangswicklungen des Summenwandlers so gestaltet sein, dass die Eingangsströme entsprechend gewichtet werden. Nehmen wir dazu ein einfaches Beispiel an, bei dem der Hauptwandler I die Übersetzung 1000/5 A und der Hauptwandler II die Übersetzung 100/5 A hat. Die Eingänge des Summen-Stromwandlers müssen nun so gestaltet sein, dass der Strom am Eingang I zehnmal stärker gewichtet in die Summe eingeht als der Strom am Eingang II. Deshalb müssen bei der Bestellung von Summenwandlern für ungleiche Hauptwandler immer die Übersetzungen der einzelnen Hauptwandler angegeben werden. Die Primäranschlüsse dieser Summenwandler sind dann immer nur einem bestimmten Hauptwandler zugeordnet und dürfen keinesfalls vertauscht werden. Doch gleichgültig, um welche Art von Summenwandlers es sich handelt, lässt sich die Gesamtübersetzung krgaus der Kombination von Haupt- und Summenwandler stets aus der folgenden, einfachen Betrachtung herleiten:
Der sekundäre Bemessungsstrom IsrS des Summenwandlers repräsentiert stets die Summe aller Primärströme der Hauptwandler, den Gesamtprimärstrom IprHg. Somit folgt allgemein für die Gesamtübersetzung
Natürlich entspricht die Gesamtübersetzung krgnach Gleichung 19/S.82 auch dem Gesamt-Wandlerfaktor bzw. dem Gesamt-Zählerfaktor cg. Bei der Bestimmung der Übersetzung und des Wandlerfaktors ist davon auszugehen, dass eventuell vorhandene offene Eingänge auch beschaltet, jedoch momentan stromlos sind.
7.5.2.1 ZAHLENBEISPIELE ZUR ERMITTLUNG DER GESAMTÜBERSETZUNG
a) Beispiel für gleiche Hauptwandler
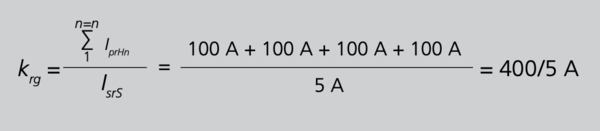
Ausgehend von vier Hauptwandlern mit der Bemessungsübersetzung krHn = 100/5 A und einem Summenwandler mit der Bemessungsübersetzung krS = 4 × 5/5 A gilt nach Gleichung 26/S. 101
Aus Gleichung 26 folgt
b) Beispiel für ungleiche Hauptwandler
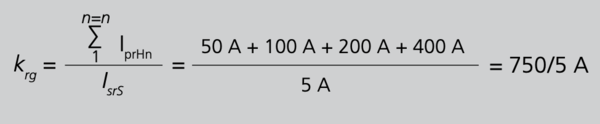
Vier ungleiche Hauptwandler mit den Bemessungsübersetzungen krH1=50⁄5 A, krH2=100⁄5 A, krH3=200⁄5 A und krH4=400⁄5 A. Der Ausgangsstrom des Summenwandlers betrage ebenfalls IsrS= 5 A. Nach Gleichung 26/S.101 folgt 102
Aus Gleichung 26 folgt
7.5.3 LEISTUNGSANFORDERUNG AN DIE HAUPTWANDLER
Ein Summen-Stromwandler soll die Bemessungsleistung SrS abgeben können. Dazu muss er zum einen konstruktiv in der Lage sein, diese Leistung abgeben zu können. Zum anderen kann ein Summenwandler aber nur die Leistung weitergeben, die ihm geliefert wird. Es ist also sicherzustellen, dass die Bemessungsleistungen SrHnder einzelnen n Hauptwandler ausreichend hoch sind. Dabei dürfen die Verluste des Summenwandlers SvS(bei Bemessungs- strom) und die der Zuleitung zwischen Haupt- und Summenwandler nicht vernachlässigt werden. Der Leistungsverlust PLr der Zuleitungen kann anhand der Gleichung 23/S.85 berechnet werden mit anschließender Addition von 0,1 W pro Anschlussklemme für mögliche Übergangswiderstände an diesen. Je Hauptwandler ergeben sich vier Anschlussklemmen, zwei am Hauptwandler-Ausgang selbst und zwei am Summenwandler-Eingang. Auch müssen die Hauptwandler die Eigenverluste des Summenwandlers liefern. Sind diese nicht bekannt, so hat sich in der Praxis als Abschätzung bis zu einer Bemessungsleistung von SrS = 15 VA bewährt, je Eingang pauschal rund 2 VA anzunehmen. Die Eigenverluste eines Summenwandlers mit beispielsweise vier Eingängen betragen dann also insgesamt 8 VA.
Die Bemessungs-Ausgangsleistung SrSdes Summenwandlers verteilt sich auf die Hauptwandler im Verhältnis der Teil-Sekundärströme IsrSn,
die am Summenwandler-Ausgang wirksam werden zum sekundären Bemessungsstrom IsrS, nach Gleichung 27/S. 104 also
Gleichung 27
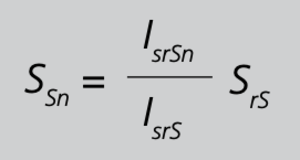
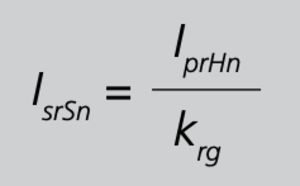
Der sekundäre Teilstrom IsrSnist der von einem Hauptwandler verursachte Anteil des am Summenwandler-Ausgang fließenden gesamten Sekundärstroms IsrS. Hierbei gilt für diesen Teilstrom
Gleichung 28
IprHg= Gesamtprimärstrom aller n Hauptwandler
IsrSn = sekundärer Teilstrom des Summenwandlers, verursach durch den n-ten Hauptwandler
krg= Gesamtübersetzung Summenwandlers, verursach durch den n-ten Hauptwandler
SSn= Anteil des n-ten Hauptwandlers an der Bemessungsleistung des Summen-Stromwandlers
IsrS= sekundärer Bemessungsstrom des Summen-Stromwandlers
Anmerkung: Wirk- und Scheinleistungen sowie unterschiedliche Scheinleistungen dürfen nicht arithmetisch addiert werden. Hier sind i.Allg. nur Zeigeradditionen zulässig. Obwohl dieser Umstand bei der Näherungsgleichung 30/S.105 vernachlässigbar ist, darf hier kein Gleichheitszeichen verwendet werden.
7.5.3.1 ZAHLENBEISPIELE ZUR ERMITTLUNG DER BEMESSUNGSLEISTUNGEN DER HAUPTWANDLER
Auch hier sollen zwei Beispiele für mehr Klarheit sorgen.
a) Beispiel für gleiche Hauptwandler
Wir übernehmen die Daten des Summenwandlers aus dem Kapitel 7.5.2.1/S.102, die wir um eine geforderte Leistung von z.B. SrS= 5 VA ergänzen und fragen nach den von den Hauptwandlern zu fordernden Leistungen SHn. Wir nehmen für die Eigenverluste des Summenwandlers SvS= 8 VA und für die Leitungsverluste PLr=1 W pro Pfad an. Für die Gesamtübersetzung hatten wir bereits mit Gleichung 26/S.101 krg=400⁄(5 A=80) ermittelt. Nunmehr folgt nach 28/S.104 für den sekundären Teilstrom, verursacht durch den ersten Hauptwandler
Aus Gleichung 28 folgt
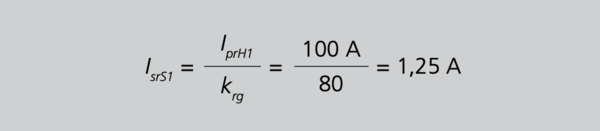
Da alle Hauptwandler identisch sind, gilt der gleiche Teilstrom auch für die übrigen Wandler. Mit 29/S.105 erhalten wir für die Verluste des Summenwandlers, die der erste Hauptwandler anteilig tragen muss.
Aus Gleichung 29 folgt
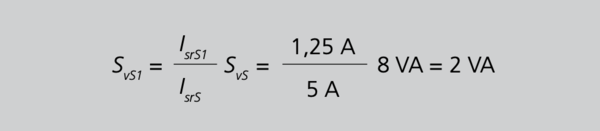
Auch hier gilt der gleiche Verlustanteil für alle anderen Hauptwandler. Nach 27/S.104 beträgt der Leistungsteil, den der erste Hauptwandler an der Bemessungsleistung des Summenwandler beitragen muss
Aus Gleichung 27 folgt
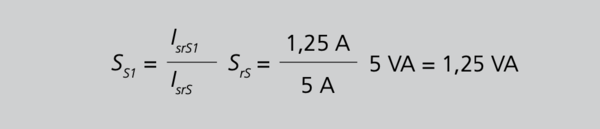
Mit 30/S. 105 folgt dann für die vom ersten Hauptwandler zu fordernde Leistung
Aus Gleichung 30 folgt
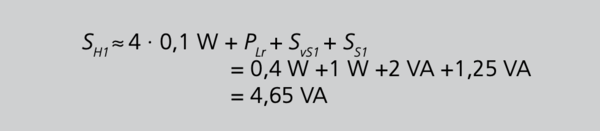
Es muss daher von jedem Hauptwandler eine Leistung von 4,65 VA gefordert werden, aufgerundet auf die nächstgelegene Bemessungsleistung also 5 VA.
b) Beispiel für ungleiche Hauptwandler
Wir übernehmen diesmal die Daten des Summenwandlers für ungleiche Hauptwandler aus dem Kapitel 7.5.2.1/S.102, die wir um eine geforderte Leistung von z. B. wiederum SrS = 5 VA ergänzen, und fragen nach den von den einzelnen Hauptwandlern zu fordernden Leistungen SHn. Auch soll für Eigen- und Leitungsverluste wieder gelten SvS = 8 VA und PLr=1 W pro Pfad. Die Gesamtübersetzung beträgt krg = 750⁄ (5 A =150). Nach 28/S. 106 folgt für die einzelnen sekundären Teilströme, die die Hauptwandler am Summenwandler-Ausgang verursachen
Aus Gleichung 28 folgt
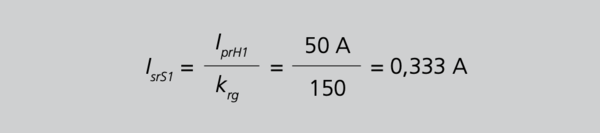
Aus Gleichung 28 folgt
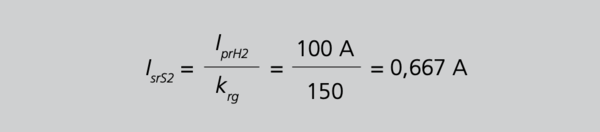
Aus Gleichung 28 folgt
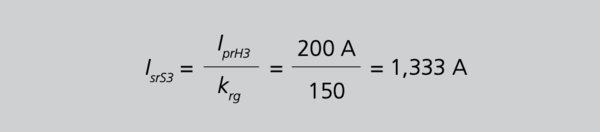
Aus Gleichung 28 folgt
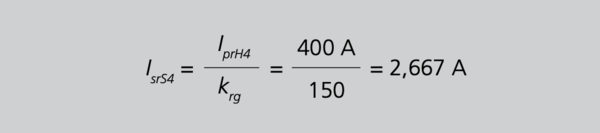
Es sollte nicht wundern, dass die Summe aller Teilströme (bis auf eventuelle Rundungsfehler) wieder 5 A beträgt. Die Verluste des Summenwandlers verteilen sich auf die Hauptwandler gemäß 29/S.107.
Aus Gleichung 29 folgt

Aus Gleichung 29 folgt
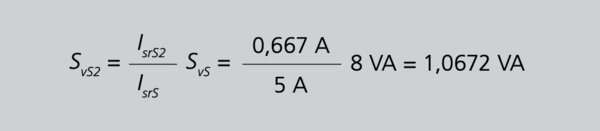
Aus Gleichung 29 folgt

Aus Gleichung 29 folgt

Zur Kontrolle muss die Summe aller Teilleistungen (bis auf eventuelle Rundungsfehler) wieder 8 VA ergeben. Nach 27/S.104 beträgt der Leistungsteil, den die Hauptwandler an der Bemessungsleistung des Summenwandler beitragen müssen
Aus Gleichung 27 folgt
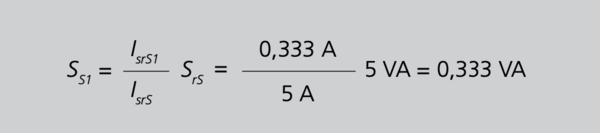
Aus Gleichung 27 folgt
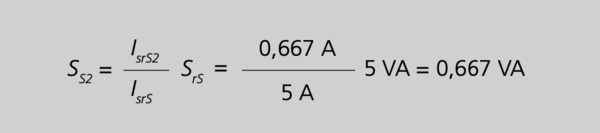
Aus Gleichung 27 folgt

Aus Gleichung 27 folgt

Mit 30/S. 105 folgt dann letztendlich für die von den Hauptwandlern zu fordernden Leistungen
Aus Gleichung 30 folgt

Aus Gleichung 30 folgt

Aus Gleichung 30 folgt

Aus Gleichung 30 folgt

Wir erhalten in der Summe aller Leistungen der Hauptwandler wieder dasselbe Ergebnis wie bei gleichen Hauptwandlern (bis auf eventuelle Rundungsfehler). Hier verteilt sich die Leistung jedoch unterschiedlich auf die einzelnen Hauptwandler. Es müssen also Hauptwandler mit den nächstgelegenen genormten Bemessungsübersetzungen bestellt werden, im Einzelnen:
· Wandler 1: 50/5 A, 2,5 VA
· Wandler 2: 100/5 A, 5 VA
· Wandler 3: 200/5 A, 5 VA
· Wandler 4: 400/5 A, 10 VA
7.5.4 GENAUIGKEITSBETRACHTUNG BEI DER KOMBINATION VON HAUPT- UND SUMMEN-STROMWANDLERN
Für die Hintereinanderschaltung von Haupt- und Summenwandlern gelten nachfolgende Aussagen, ohne hier auf die Herleitung einzugehen. Wer sich für die konkrete Herleitung interessiert, sei an das Literaturverzeichnis (z.B. [4]) verwiesen. Die Fehlwinkel werden addiert und näherungsweise auch die Stromfehler. Nicht beschaltete Eingänge müssen offen bleiben, wie bereits erwähnt. Bei der Bestimmung des Wandlerfaktors ist davon auszugehen, dass auch offene Eingänge beschaltet, jedoch momentan stromlos sind.
Die Fehlwinkel werden addiert und näherungsweise auch die Stromfehler.
7.5.5 SUMMEN-STROMWANDLER ALS ANPASSWANDLER
Als Beispiel soll die Addition von 3 Hauptwandlern mit den Übersetzungen von jeweils krH=300/5 A angenommen werden. Als Gesamtübersetzung gilt dann gemäß 26/S.101 krg=900/5 A. Diese Gesamtübersetzung kann Probleme verursachen, z.B. beim Anschluss eines Analoginstruments, wenn diese Skalierung nicht geliefert werden kann. Auch gibt es elektronische Stromzähler, bei denen die Eingabe dieses Zählerfaktors nicht möglich ist. Ebenfalls bei klassischen mechanischen Zählern, bei denen man noch manuell die Anzeige mit dem Zählerfaktor multiplizieren muss, ist die Multiplikation mit dem Zählerfaktor von cg= 180, der sich in diesem Beispiel ergibt, unpraktisch. Ein Wandlerhersteller ist aber in der Lage, einen Summenwandler derart zu modifizieren, dass hier die Übersetzung krg = 900/4,5 A lautet. Als ungekürzter Bruch entspricht dies der Übersetzung krg= 1000/5 A und einem Zählerfaktor von cg = 200. Man kann also einen Summen-Stromwandler auch gleichzeitig zum Anpassen einer wenig geeigneten Gesamtübersetzung an eine besser geeignete verwenden.
7.5.6 SUMMIERUNG OHNE SUMMEN-STROMWANDLER
Das Kapitel über Summen-Stromwandler sei noch um die Erkenntnis ergänzt, dass man die Sekundärströme von Hauptwandlern gleicher Stränge auch ohne Summenwandler addieren kann. Voraussetzung hierbei ist jedoch, dass alle Hauptwandler gleich sind. In diesem Fall werden die Ausgänge aller Wandler parallelgeschaltet. Hier findet jedoch keine Transformation der Ausgangsgröße statt, sodass zu prüfen ist, ob die nachfolgenden Gerätschaften für den höheren Strom verwendet werden können. Letztlich kann man hier mit einem Wickel-Stromwandler in Form eines Zwischenwandlers den Sekundärstrom anpassen. Es besteht auch die Möglichkeit, Hauptwandler mit kleineren Ausgangsströmen zu verwenden. So können z.B. zwei Stromwandler mit einem Sekundärstrom von jeweils 2,5 A zu einem Gesamt-Sekundärstrom von 5 A addiert werden. Anmerkung: Die hier vorgestellte Summierung ohne Summen-Stromwandler darf nicht mit der Holmgreen-Schaltung verwechselt werden. Hierbei befinden sich die Stromwandler auf den drei Strängen L1, L2 und L3 eines Systems und liefern durch Addition der Sekundärströme im fehlerfreien Zustand die Summe Null. Wer mehr über diese Schaltung erfahren möchte, sei an das Literaturverzeichnis (z.B. [4]) verwiesen.
LITERATURVERZEICHNIS
- DIN EN 61869-1 (VDE 0414-9-1), Messwandler, Beuth Verlag GmbH, Berlin
- DIN EN 61869-2 (VDE 0414-9-2), Messwandler, Beuth Verlag GmbH, Berlin
- Alois Bröder, Strom-Messwandler, Grundlagen und Berechnungs- verfahren, 2017, Shaker-Verlag, ISBN 978-3-8440-5649-5
- Alois Bröder, Strom-Messwandler, Informationen für Anwender, 2018, Shaker-Verlag, ISBN 978-3-8440-6233-5
- Rolf Fischer, Elektrische Maschinen, 2011, Carl Hanser Verlag, ISBN 978-3-446-42554-5
- Rudolf Bauer, Die Messwandler, 1953, Springer-Verlag, ISBN 978-3-662-11515-2
- Isaac Goldstein, Die Meßwandler, 1928, Springer-Verlag, ISBN-13: 978-3-642-89761-0
- Martin Kahmann, Elektrische Energie elektronisch gemessen, 1994, VDE-Verlag, ISBN 978-3800718597
- Ingmar Grambow (Hrsg.), Messwandler für Mittel- und Hoch- spannungsnetze, 2000, expert-Verlag (Kontakt & Studium, Band 554), ISBN 3-8169-1587-6
- Ungrad, Winkler, Wiszniewski, Schutztechnik in Elektroenergie- systemen, 1994, Springer-Verlag, ISBN 978-3-642-63409-3
- Fachwörterbuch Messwandler, Autorenkollektiv der Ritz Instrument Transformer GmbH, 2010, Union Druckerei Dresden GmbH
DAS KLEINE EINMALEINS DER STROMWANDLER
Herausgeber: REDUR GmbH & Co. KG
Autor: Alois Bröder
© Copyright REDUR GmbH & Co. KG
1. Auflage, Dezember 2020
Für Irrtümer und Druckfehler wird keine Haftung übernommen. Verwendete Bilder und Markennamen sind Eigentum der Rechtsinhaber oder des Autors. Änderungen in Technik und Ausführung behalten wir uns vor. Nachdruck, auch nur auszugsweise, ist genehmigungspflichtig. Es gelten die allgemeinen Geschäftsbedingungen unter www.redur.de/agb/
ISBN: 978-3-00-068179-0
Gestaltungskonzeption
KÖHLER & PARTNER
www.koehler-partner.de
Widmung
Wir danken dem Autor Alois Bröder für die sehr gelungene Zusammenstellung des Einmaleins der Stromwandler. Herr Bröder gilt nicht nur als Schöpfer der kompaktesten und vielseitigsten Stromwandler, sondern auch als begnadeter Lektor und Mentor. In seinem kompletten Berufsleben und darüber hinaus als Pensionär widmete und widmet er sich der Technik der Stromwandler. Er ist für seinen unermüdlichen Einsatz, die teilweise komplexe technische Materie der Stromwandler einem breiten Publikum näher zu bringen, über die Landesgrenzen hinaus bekannt. Ich persönlich bedanke mich für alles, was Herr Bröder für die REDUR, Kunden, Mitarbeiter und Stromwandlerfans aus aller Welt im Laufe der letzten Jahrzehnte geleistet hat.
Dr. Lothar Schunk
Geschäftsführer REDUR GmbH. Co. KG