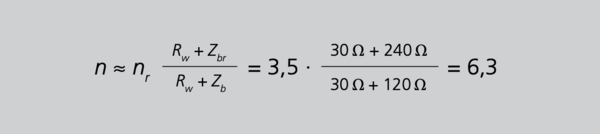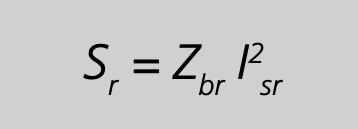3. WICHTIGE BEMESSUNGSGRÖSSEN
Bei den Bemessungsgrößen (früher Nenngrößen) findet man heute die Indizes „r“ für „rated“, engl. für bemessen. Nachfolgende Bemessungsgrößen charakterisieren einen Stromwandler.

3.1 PRIMÄRER UND SEKUNDÄRER BEMESSUNGSSTROM Ipr UND Isr , BEMESSUNGSÜBERSETZUNG kr
Primärer und sekundärer Bemessungsstrom (früher Nennstrom, engl. rated current) sind die auf dem Leistungsschild (Abb.17/S.33) angegebenen Stromwerte,
· die den Stromwandler kennzeichnen,
· für die der Stromwandler bemessen ist,
· auf die sich weitere Charakteristika des Stromwandlers beziehen.
Nach der DIN EN 61869-2 sind genormte Bemessungs-Sekundärströme 1 A und 5 A . Seltener gibt es, bedingt durch die vorhergegangenen Normen, noch 2 A und die durch √3 geteilten Normwerte für Stromwandler mit im Dreieck geschalteten Sekundärwicklungen. Genormte Bemessungs-Primärströme sind 10; 12,5; 15; 20; 25; 30; 40; 50; 60; 75 A, sowie deren dezimale Vielfache und Teile davon. Da Normen im Gegensatz zu Gesetzen nicht bindend sind, sind auch andere Bemessungsströme, z.B. 2,5 A durchaus möglich. Auch kann die Sekundärgröße eine Spannung sein, die an einem internen Widerstand aus dem Sekundärstrom gewonnen wird (Sensoren, Kapitel 2.3/S. 22). Primärer und sekundärer Bemessungsstrom werden als ungekürzter Bruch angegeben und bilden so die Bemessungsübersetzung (früher Nennübersetzung, engl. rated transformation ratio)
Gleichung 5
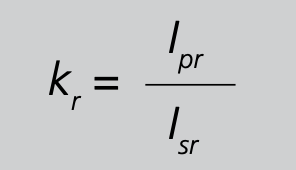
kr = Bemessungsübersetzung
Ipr= primärer Bemessungsstrom
Isr= sekundärer Bemessungsstrom
Eine korrekte Angabe sollte eigentlich z. B. 200 A/5 A lauten. Es hat sich aber die Schreibweise 200/5 A eingebürgert. Bei einem idealen, fehlerfreien Stromwandler drückt die Bemessungsübersetzung das Verhältnis eines jeden beliebigen Primärstroms Ipzum Sekundärstrom Isinnerhalb eines definierten Strombereichs (dem Arbeitsbereich) aus. Gleichung 2/S.12 gilt daher nur für den idealen, fehlerfreien Stromwandler. Ein idealer Stromwandler mit der Bemessungsübersetzung von z.B. kr= 200⁄5 A liefert folgerichtig nach dieser Gleichung bei einem Primärstrom von Ip = 100 A einen Sekundärstrom von Is = 2,5 A.
3.2 THERMISCHER BEMESSUNGS-KURZZEITSTROM Ith
Ein Stromwandler muss im Stromnetz auftretende, kurzzeitige Überströme, wie sie z. B. bei Kurzschlüssen entstehen, schadlos überbestehen können. Der Effektivwert des Primärstroms, den der Wandler bei kurzgeschlossener Sekundärwicklung eine Sekunde lang aushalten muss, ohne Schaden zu nehmen, heißt thermischer Bemessungs-Kurzzeitstrom (engl. rated short-time thermal current). Als thermischer Bemessungs-Kurzzeitstrom wird häufig der 60-fache Bemessungsstrom gefordert. Bei Mittelspannungswandlern ist oft sogar der Faktor 100 oder ein höherer anzutreffen. Ith muss nicht zwingend als Faktor des Bemessungsstroms angegeben werden. Die Angabe in kA ist ebenfalls zulässig und bei Mittelspannungswandlern üblich. Beim thermischen Bemessungs-Kurzzeitstrom steht die Wärmeentwicklung im Vordergrund, während es bei dem nachfolgenden Bemessungs-Stoßstrom in erster Linie auf die Kraftentwicklung ankommt, die das durch die Ströme verursachte Magnetfeld ausübt.
3.3 BEMESSUNGS-STOSSSTROM Idyn
Beim Bemessungs-Stoßstrom (engl. rated dynamic current) handelt es sich um den Scheitelwert der ersten Amplitude des Primärstroms, dessen magnetischer Kraftwirkung der Stromwandler bei kurzgeschlossener Sekundärwicklung ohne Beschädigung standhält. Das gilt bei einem Aufsteck-Stromwandler nicht für die Umbruchkräfte, die das Schienensystem entwickelt. Es ist darauf zu achten, dass die auftretenden Kurzschlusskräfte der Schienen durch zusätzliche Stützer abgefangen werden müssen. Typisch für den Bemessungs-Stoßstrom ist der Wert des 2,5-fachen thermischen Bemessungs-Kurzzeitstroms. Nur bei Abweichung von diesem Wert muss der Bemessungs-Stoßstrom auf dem Leistungsschild angegeben werden. Trotzdem wird er häufig auch dann angegeben in der Form Idyn= 2,5 · Ith.
3.4 THERMISCHER BEMESSUNGS-DAUERSTROM Icth
Der thermische Bemessungs-Dauerstrom (engl. rated continuous thermal current) ist der Primärstrom, mit dem der Wandler bei Bemessungsbürde (Kapitel 3.10/S.51) dauerhaft betrieben werden kann, ohne die Anforderungen der Genauigkeitsklasse (Kapitel 4/S. 21) zu verletzen und ohne die Spezifikation der Isolierstoffklasse (Kapitel 5.4/S. 73) zu überschreiten. Genormte thermische Bemessungs-Dauerstromstärken sind 100 %, 120 %, 150 % und 200 % des Bemessungsstroms. Obwohl sich die Angabe des thermischen Bemessungs-Dauerstroms gemäß der Norm auf den Primärstrom bezieht, ist es im Grunde genommen aber belanglos, ob die Basis der primäre oder sekundäre Bemessungsstrom ist, da dieser i. Allg. in Prozent des Bemessungsstroms angegeben wird. So kann man z. B. bei einem Wandler mit der Übersetzung 100/5 A von einem primären thermischen Bemessungs-Dauerstrom von 120 A reden oder einem sekundären thermischen Bemessungs-Dauerstrom von 6 A . Beträgt der thermische Bemessungs-Dauerstrom 100 % des Bemessungsstroms, kann diese Angabe auf dem Typenschild entfallen. Für alle anderen thermischen Bemessungs-Dauerströme wurden ergänzend zur Genauigkeitsklasse die Bezeichnungen „ext.120 %“; „ext.150 %“; „ext.200 %“ eingeführt. In den allermeisten Fällen ist 120 % üblich. Der thermische Bemessungs-Dauerstrom von 100 % ist erst vor wenigen Jahren zusätzlich in die Norm aufgenommen worden.
3.5 ÜBERSETZUNGSMESSABWEICHUNG ε
Die Übersetzungsmessabweichung (engl. current error, ratio error) eines Stromwandlers, auch Stromfehler genannt, ausgedrückt in Prozent, ist definiert durch die Gleichung 6/S. 38, wie sie auch in der DIN EN 61869-2 zu finden ist.
Gleichung 6

ε = Stromfehler
kr= Bemessungsübersetzung
Ip= Primärstrom
Is= Sekundärstrom
I‘p= auf die Sekundärseite bezogener Primärstrom, bzw. idealer Sekundärstrom

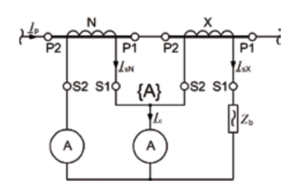
Hier ist zu beachten, dass im Zähler der Gleichung 6/S. 38 eine reine Betragsaddition der Effektivwerte stattfindet, im Gegensatz zur Gesamtmessabweichung (Kapitel 3.7/S.41). Abb.18/S.39 verdeutlicht den Stromfehler anhand einer typischen Messschaltung, wobei in der praktischen Anwendung im Primärkreis natürlich kein Amperemeter vorhanden ist. Die beiden Amperemeter messen jeweils die Effektivwerte von Primär- und Sekundärstrom, ohne Berücksichtigung der durch den Wandlerfehler bedingten Phasenverschiebung zwischen diesen beiden Strömen. Die Messschaltung erfüllt in ihrer Funktion die Gleichung 6/S.38. Im Umkehrschluss wird deutlich, dass bei der Messung des Effektivwerts des Sekundärstroms der dabei auftretende Messfehler der Stromfehler ist, abgesehen vom Fehler des Messgeräts. Die Division von Zähler und Nenner des Bruchs in 6/S.38 durch die Bemessungsübersetzung kr liefert
aus Gleichung 6
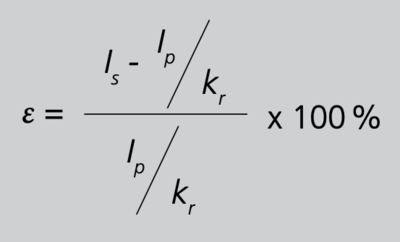
und mit Gleichung 3/S.13.
Gleichung 7
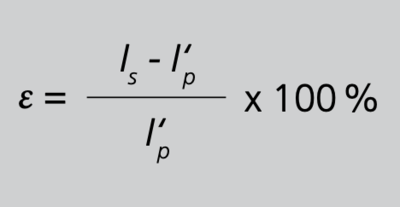
Die Betrachtung der Übersetzungsmessabweichung ε lässt sich also auf die linke Seite des ESBs (Abb. 5/S. 11) reduzieren. Die arithmetische Differenz von tatsächlichem Sekundärstrom Is und idealem Sekundärstrom I‘p, bezogen auf den idealen Sekundärstrom liefert ebenfalls die Übersetzungsmessabweichung. Um hier Missverständnissen vorzubeugen, sei noch einmal darauf hingewiesen, dass es sich bei der arithmetischen Differenz von tatsächlichem Sekundärstrom und idealem Sekundärstrom nicht um den Fehlerstrom Iε handelt! Letztere ergibt sich aus der geometrischen Differenz, also der Subtraktion der Stromzeiger von I‘p und Is.
3.6 FEHLWINKEL Δφ
Wie ein Transformator enthält auch ein Stromwandler interne parasitäre Elemente wie Eisenverlustwiderstand, Streuinduktivität und Wicklungswiderstand (siehe auch ESB Abb.5/S.11). Diese Komponenten verursachen neben dem Stromfehler auch eine Phasenverschiebung zwischen Primär- und Sekundärstrom, den Fehlwinkel (engl. phase displacement), auch Winkelfehler genannt. Spielt der Fehlwinkel bei der reinen Strommessung auch keine Rolle, so macht er sich bei der Leistungs- und Energiemessung als zusätzlicher Fehler bemerkbar. Auch beim Betrieb von phasenempfindlichen Schutzeinrichtungen wie z.B. bei Richtungsschutzgeräten, verdient der Fehlwinkel besondere Beachtung. Der Fehlwinkel wird in Winkelminuten angegeben. Bekanntlich kann man die Zeitachse einer Periode des Wechselstroms auch mit 360° beschreiben. Ein Grad hat dabei 60 Minuten als kleinere Einheit. Alternativ kann der Winkelfehler auch in Centiradiant beschrieben werden (1 crad = 34,4 min). Der Winkelfehler ist positiv definiert, wenn die sekundäre Größe voreilt.
3.7 GESAMTMESSABWEICHUNG εc
Bei der Gesamtmessabweichung (engl. composite error) handelt es sich im Gegensatz zur Übersetzungsmessabweichung ε um den Betrag der zeigerrichtigen Differenz von tatsächlichem und idealem Sekundärstrom, bezogen auf den Betrag des idealen Sekundärstroms. Damit geht Gleichung 7/S.39 über in
Gleichung 8

Im Zähler dieser Gleichung handelt es sich um den Fehlerstrom Iε, denn wie aus dem ESB (Abb.5/S. 11) leicht zu erkennen, gilt
Gleichung 9
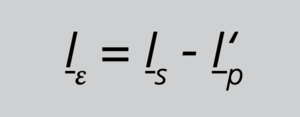
und mit Gleichung 8/S.41 folgt damit
Gleichung 10

Auch Gleichung 8/S.41 oder Gleichung 10/S.42 lassen sich auf den Primärstrom beziehen, analog zu Gleichung 6/S.39. Dazu braucht nur der Bruch mit der Bemessungsübersetzung kr erweitert zu werden.
Somit folgt aus Gleichung 8
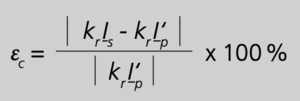
und mit Gleichung 3/S.13 folgt damit
Gleichung 11
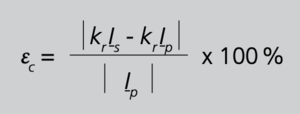
Sofern in der Praxis die Gesamtmessabweichung εc betrachtet wird, befindet sich der Kern oft nahe der Sättigung und somit im nichtlinearen Bereich des Übertragungsverhaltens eines Wandlers. Fehlerstrom und Primärstrom sind dann häufig stark mit Oberwellen behaftet. Zeigerdarstellungen sind jedoch nur bei sinusförmigen Verläufen sinnvoll. Daher ist in der DIN EN 61869-2 als Definition der Gesamtmessabweichung die Gleichung
Gleichung 12
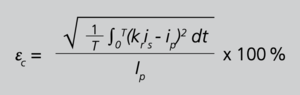
εc = Gesamtmessabweichung
Is= (komplexer) Zeiger des Sekundärstroms
I‘p = (komplexer) Zeiger des auf die Sekundärseite bezogenen Primärstroms, bzw. des idealen Sekundärstroms
Iε = (komplexer) Zeiger des Fehlerstroms
kr = Bemessungsübersetzung
Iε = (komplexer) Zeiger des Fehlerstroms
εc= Gesamtmessabweichung
Is= (komplexer) Zeiger des Sekundärstroms
I‘p= (komplexer) Zeiger des auf die Sekundärseite bezogenen Primärstroms, bzw. des idealen Sekundärstroms
εc = Gesamtmessabweichung
kr = Bemessungsübersetzung
Is = (komplexer) Zeiger des Sekundärstroms
I‘p= (komplexer) Zeiger des auf die Sekundärseite bezogenen Primärstroms, bzw. des idealen Sekundärstroms
Ip = (komplexer) Zeiger des Primärstroms
εc= Gesamtmessabweichung
Iε= (komplexer) Zeiger des Fehlerstroms
T = Periodendauer
is = Sekundärstrom (Momentanwert)
Is= (komplexer) Zeiger des Sekundärstroms
kr= Bemessungsübersetzung
Ip= (komplexer) Zeiger des Primärstroms
ip, Ip= Primärstrom (Momentanwert und Effektivwert)
zu finden, die für rein sinusförmige Ströme mit Gleichung 11/S.43 übereinstimmt. Auf Gleichung 12/S.44 soll hier nicht näher eingegangen werden. Wer hierzu weitere Informationen möchte, sei an das Literaturverzeichnis (z.B. [3] oder [4]) verwiesen. Die Gesamtmessabweichung ist für den Anwender insofern von Bedeutung, als sich Bemessungs-Begrenzungsstrom und Bemessungs-Genauigkeitsgrenzstrom (Kapitel 3.8/S.46) auf sie beziehen. Obwohl der Stromfehler positiv oder negativ sein kann, ergibt sich für die Gesamtmessabweichung immer eine positive Größe, da Effektivwerte stets positiv sind.
Zum besseren Verständnis der Gesamtmessabweichung soll noch eine einfache Messschaltung betrachtet werden am Beispiel eines Stromwandlers mit der Übersetzung 1:1, wie in Abb.19/S.45 gezeigt. Sowohl der Primär- als auch der (bis auf den Fehler) gleich große Sekundärstrom durchfließen das Amperemeter, jedoch in unterschiedlichen Richtungen, sodass eine Subtraktion beider Ströme stattfindet. Nach der ersten kirchhoffschen Regel (Knotenregel) gilt für Punkt {A}, dass bei phasenrichtiger Addition aller Ströme die Summe Null ergibt. Somit folgt hier als Differenz der tatsächliche Fehlerstrom und kann bei reinen Sinusgrößen geschrieben werden als
Gleichung 13
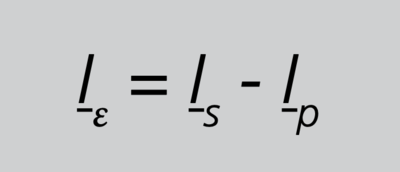
Achtung! Gleichung 13/S.45 gilt nur für das hier betrachtete Beispiel mit dem Sonderfall der Bemessungsübersetzung von 1:1. Abgeleitet aus dem ESB (Abb.5/S.11) gilt allgemeingültig Gleichung 9/S.42. Beim Vergleich der Gleichungen 6/S.38 und 11/S.43 wird der Unterschied zwischen Übersetzungsmessabweichung ε und Gesamtmessabweichung εc nochmals deutlich. Während bei der Übersetzungsmessabweichung im Zähler der Gleichung die arithmetische Differenz der Effektivwerte von mit der Bemessungsübersetzung multipliziertem Sekundärstrom und Primärstrom zu sehen ist, werden bei der Gesamtmessabweichung vor der Betragsbildung diese Größen erst zeigerrichtig, also vektoriell, subtrahiert.
3.8 BEMESSUNGS-BEGRENZUNGSSTROM IPL , BEMESSUNGS-GENAUIGKEITSGRENZSTROM, ÜBERSTROM-BEGRENZUNGSFAKTOR FS, GENAUIGKEITSGRENZFAKTOR ALF
Weder der Bemessungs-Begrenzungsstrom IPL (engl. excitation current) bei Strom-Messwandlern noch der Bemessungs-Genauigkeitsgrenzstrom (engl. rated accuracy limit primary current) bei Schutz-Stromwandlern müssen auf dem Typenschild angegeben werden. Der Bemessungs-Begrenzungsstrom ist der Primärstrom eines Messwandlers, bei dem die Gesamtmessabweichung des Sekundärstroms 10% beträgt. Damit lässt sich der Überstrom-Begrenzungsfaktor (engl. instrument security factor) definieren als das Verhältnis des Bemessungs-Begrenzungsstroms zum primären Bemessungsstrom. Der Überstrom-Begrenzungsfaktor (engl.: instrument security factor) oder kurz Überstromfaktor gibt an, ab dem Wievielfachen des Bemessungsstroms ein Messwandler in Sättigung geht. Hierzu gilt die Bezeichnung FS 5 oder FS 10. Zur Abgrenzung gegen Schutzwandler hieß die Bezeichnung früher M 5 oder M 10 (M für Messwandler). FS 5 sagt, dass der Wandler spätestens beim fünffachen Bemessungsstrom in Sättigung gehen muss, bei FS 10 entsprechend beim zehnfachen, vorausgesetzt, der Wandler ist mit der Bemessungsbürde belastet. Exakt definiert ist dieser Punkt durch die Beschreibung, dass beim fünffachen Bemessungsstrom (bzw. zehnfachen) die Abweichung vom idealen, fehlerfreien Stromverlauf, bezogen auf die Gesamtmessabweichung εc, mindestens 10 % betragen muss (nach DIN EN 61869-2). Der Bemessungs-Genauigkeitsgrenzstrom bei Schutzwandlern ist das Pendant zum Bemessungs-Begrenzungsstrom eines Messwandlers, also der Wert des Primärstroms eines Schutz-Stromwandlers, bis zu dem dieser die Genauigkeitsanforderung erfüllt. Demzufolge entspricht dem Genauigkeitsgrenzfaktor eines Schutzwandlers der Überstrom-Begrenzungsfaktor eines Messwandlers. Während also Messwandler oberhalb des Bemessungsstroms möglichst rasch in Sättigung gehen sollen, um ein Anwachsen des Sekundärstroms im Fehlerfall zu vermeiden, wird bei Schutzwandlern eine möglichst weit außerhalb des Bemessungsstroms liegende Sättigung verlangt. Wann die Sättigung erreicht ist, ist bei Schutzwandlern durch den Genauigkeitsgrenzfaktor ALF (engl. accuracy limiting factor) ausgedrückt in Verbindung mit dem vorausgehenden Buchstaben „P“ (engl.: protection) und der Genauigkeits-Klassenangabe. So bedeutet z.B. 5P10, dass beim zehnfachen Bemessungsstrom der Fehler, bezogen auf die Gesamtmessabweichung εc, höchstens 5 % betragen darf, auch wieder vorausgesetzt, der Wandler ist mit der Bemessungsbürde belastet. Nach der DIN EN 61869-2 genormte Genauigkeit-Grenzfaktoren sind 5; 10; 15; 20 und 30.
3.8.1 NUMERISCHES BEISPIEL
Hier soll ein Zahlenbeispiel für zusätzliche Klarheit sorgen anhand eines hypothetischen Stromwandlers mit nachfolgenden Werten, auf deren physikalische Zusammenhänge nicht weiter eingegangen wird, um nicht den Blick für das Wesentliche zu verlieren.
Wie schon erwähnt, ergibt sich der Fehlerstrom Iε nicht als arithmetische Differenz von auf die Sekundärseite bezogenem Primärstrom I‘p und Sekundärstrom Is. Der Fehlerstrom Iε ist die vektorielle Differenz beider. Bei diesem hypothetischen Strom-Messwandler mit der Übersetzung 100/5 A wird der Primärstrom über den Bemessungsstrom hinaus erhöht. Wir nehmen an, dass beim Primärstrom von 350 A auf der Sekundärseite statt der zu erwartenden 17,5 A nur noch ein Effektivwert von 15,925 A zu messen ist, was folgerichtig als beginnende Sättigung gedeutet wird. Der Stromfehler in diesem Arbeitspunkt beträgt nach Gleichung 6/S. 38
Dieser Stromfehler interessiert im Zusammenhang mit dem Fehler, der bei der Strommessung entsteht. Die die Begrenzung beschreibenden Größen beziehen sich jedoch auf die Gesamtmessabweichung. Die Gesamtmessabweichung εc ergibt sich nach Gleichung 10/S.42 oder 11/S.43 zu

Damit ist der Primärstrom von 350 A also der Bemessungs-Begrenzungsstrom IPL und der Faktor 3,5 der Überstrom-Begrenzungsfaktor FS. Es wird jedoch nicht FS 3,5 angegeben, sondern normgerecht FS 5. Man sieht, dass die Gesamtmessabweichung εc größer ist als der Betrag des Stromfehlers ε. Den Betrag von 10% erreicht die Gesamtmessabweichung also vor dem Stromfehler.
3.9 BEMESSUNGSLEISTUNG Sr
Der Widerstand im Sekundärkreis setzt sich zusammen aus dem Leitungswiderstand und den Innenwiderständen der angeschlossenen Messgeräte. Wie schon in Kapitel 1.2/S. 8 erklärt, ist der Stromwandler als Konstantstromquelle anzusehen, wobei der Sekundärstrom idealerweise nur vom Primärstrom entsprechend der Übersetzung abhängt. Damit nun durch den Widerstand im Sekundärkreis der geforderte Strom fließen kann, muss der Stromwandler gemäß seiner Funktion als Konstantstromquelle die Sekundärspannung entsprechend erhöhen, um dem ohmschen Gesetz 1/S.3 gerecht zu werden.
Damit gibt der Stromwandler nach der Gleichung 14/S.50 die Leistung ab.
Gleichung 14

Die Bemessungsleistung (früher Nennleistung, engl. rated output) ist nun entsprechend Gleichung 14/S.50 diejenige Scheinleistung, für die der Stromwandler ausgelegt, also bemessen ist, und auf die sich Genauigkeit und Überstromfaktor FS beziehen. Sie wird in VA angegeben, wobei genormte Werte 1; 1,5; 2; 2,5; 5; 10; 15; 30 VA sind. Normgerecht dürfen aber auch Werte über 30 VA entsprechend dem Anwendungsfall gewählt werden. Die Bemessungsleistung beschreibt also das Leistungsvermögen eines Stromwandlers, den Sekundärstrom innerhalb der erlaubten Fehlergrenzen durch den Sekundärwiderstand „treiben“ zu können.
3.10 BÜRDE Zb , BEMESSUNGSBÜRDE Zbr
Im Sprachgebrauch der Wandlertechnik wird die Summe aller externen Scheinwiderstände im Sekundärkreis als Bürde bezeichnet. Die Bürde ist also ein Widerstand und sollte folglich mit der Einheit Ω versehen werden. Im allgemeinen Umgang wird aber häufig, historisch und umgangssprachlich bedingt, die Bürde in VA angegeben, und selbst die DIN EN 61869-2 weist unter 2.1.13 im Nebensatz darauf hin, dass die Bürde üblicherweise in VA angegeben wird. Diese stillschweigende Zustimmung zur weiteren Fortführung der fehlerhaften Terminologie ist nicht gerade hilfreich, trägt aber dem Umstand Rechnung, dass diese alte Gewohnheit nur sehr schwer aufzugeben ist. Die Bemessungsbürde Zbr (früher Nennbürde, engl. rated burden) ist der an die Sekundärklemmen anzuschließende Scheinwiderstand, für den der Stromwandler bemessen ist und der als Basis für die Genauigkeitsforderungen dient. Bei Abschluss des Stromwandlers mit der Bemessungsbürde Zbr liefert dieser bei Bemessungsstrom Isr die Bemessungsleistung Sr. Die Bemessungsbürde ist bis < 5 VA rein ohmsch und ab ≥5 VA ist sie nach Norm mit einem induktiven Blindanteil behaftet, der einem Bürdenleistungsfaktor von cosβ = 0,8 entspricht. Mit Hilfe der Bemessungsbürde kann die Bemessungsleistung auch wie folgt definiert werden, wie in der Norm DIN EN 61869-2 nachgesehen werden kann: Die Bemessungsleistung ist das Produkt aus Bemessungsbürde und dem Quadrat des sekundären Bemessungsstroms in VA, entsprechend Gleichung 15/S.52.
Gleichung 15/S.52 ist hilfreich, um einen Überblick zu gewinnen, in welcher Größenordnung sich die Werte der Bürden bei den genormten Bemessungsleistungen bewegen. Betrachtet man einen Stromwandler mit dem sekundären Bemessungsstrom von 5 A und einer Bemessungsleistung von 5 VA, so stellt man mit

fest, dass sich sogar im Milliohmbereich bewegt wird. Bei einem sekundären Bemessungsstrom von 1 A folgt analog dazu 5 Ω. Hier zeichnet sich schon ab, dass wegen des Leitungswiderstands bei großen Entfernungen Stromwandler mit 1 A-Ausgang vorzuziehen sind.
3.10.1 EINFLUSS DER BEBÜRDUNG AUF DEN ÜBERSTROM-BEGRENZUNGSFAKTOR FS
Der Überstrom-Begrenzungsfaktor, der den Schutz des Messkreises durch die natürliche magnetische Sättigung des Kerns vor zu hohen Strömen ausdrückt, hängt von der Bebürdung ab. Normgerecht definiert mit FS 5 oder FS 10 ist dieser bei Bemessungsbürde, obwohl die Sättigung tatsächlich früher einsetzen kann. Im Beispiel Kapitel 3.8.1/S.48 geschah das bereits beim 3,5-fachen Bemessungsstrom. Hier soll daher mit nr der tatsächliche Überstrom-Begrenzungsfaktor bei Bemessungsbürde und mit n der tatsächliche Überstrom-Begrenzungsfaktor bei beliebiger Bürde bezeichnet werden. Gemäß dem ESB (Abb. 5/S.11) gilt der folgende formelle Zusammenhang:
Gleichung 16

Unter der Annahme, dass der Stromwandler unter Bemessungsbedingungen beim nr-fachen Sekundärstrom in Sättigung geht und E0sat die bei Sättigung erreichte Quellenspannung ist, so geht 16/S.54 über in die Form
i

Andererseits wird die Sättigung auch bei jeder anderen Bürde, bestehend aus dem Wirkanteil Rbund dem Blindanteil Xbmit einem dazugehörenden Faktor n, für ein Vielfaches des Sekundärstroms erreicht, gemäß
ii

Gleichsetzen von (i) und (ii) liefert nach weiterer Umformung letztlich
Gleichung 17
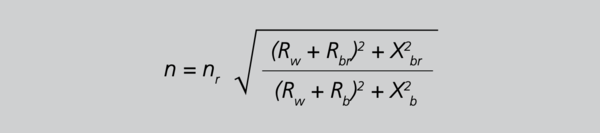
Wird der Winkel zwischen dem Wicklungswiderstand und dem Scheinwiderstand der Bürde vernachlässigt, geht die geometrische Addition in eine arithmetische über und Gleichung 17/S.55 vereinfacht sich zu 18/S.55
Gleichung 18
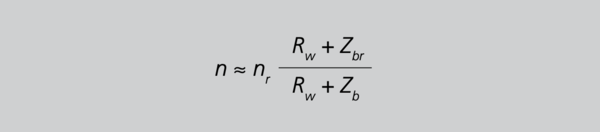
Zur Fortführung des vorherigen Beispiels aus Kapitel 3.8.1/S.48 sind folgende Ergänzungen nötig, wobei derselbe Stromwandler jetzt mit 5 VA abgeschlossen werden soll:
Mit Gleichung 17/S. 55 folgt jetzt für den tatsächlichen Überstromfaktor
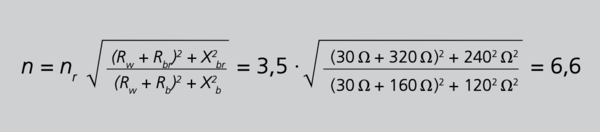
Es ist deutlich zu erkennen, dass der bisherige Überstrom-Begrenzungsfaktor von 3,5 bei 10VA (normgerecht mit FS5 angegeben) wesentlich überschritten wird. Es ist also aus Sicht des Schutzes des Sekundärkreises nicht sinnvoll, einen Wandler mit einer höheren Bemessungsleistung zu wählen als unbedingt nötig. Ist die tatsächliche Bebürdung deutlich kleiner, führt diese Unterbürdung zu einem größeren Überstrom-Begrenzungsfaktor mit möglichen unerwünschten Folgen für den Messkreis. Überschreitet die tatsächliche Bebürdung die Bemessungsbürde, spricht man von Überbürdung. Hierbei kann der Wandler bereits vor Erreichen des Bemessungsstroms in Sättigung gehen. Unterbürdung kann bei Schutzwandlern dagegen wünschenswert sein. Hier wird der Genauigkeits-Grenzfaktor als Pendant zum Überstrom- Begrenzungsfaktor von Messwandlern weiter in den Überstrombereich verschoben. Zum Abschuss dieses Beispiels sei noch die Berechnung des Überstromfaktors mit der Näherungsformel 18/S.19 durchgeführt. Der Unterschied zur Berechnung nach der exakten Gleichung 17/S.55 ist also nicht so dramatisch. Man kann daher gerne mit der Näherungsgleichung 18/S.55 arbeiten.